29. Дерево, которое знает арифметику

Математические достижения в мире деревьев не исчерпываются тем, что некоторые из них (описанные в гл. 22) ведут счет времени. В западной тропической Африке (Гана, Сьерра-Леоне, Берег Слоновой Кости) есть дерево, которое умеет умножать и складывать. Вся его жизнь может быть выражена алгебраическим уравнением.

1

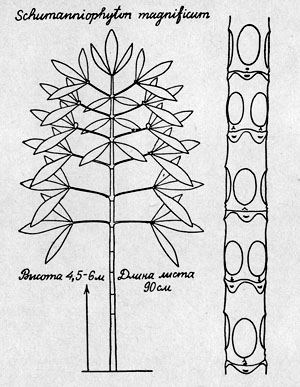
Это вовсе не шутка. Этот рисунок и фотография на стр. 337, сделанные Фрэнсисом Алле, ботаником, работавшим на Береге Слоновой Кости, помогут вам понять это замечательное дерево.

Научное название его зубодробительно — Schumanniophyton problematicum. Но как бы то ни было, видовое определение (рrоblematicum — «задачное») признает за деревом его математические способности. Оно принадлежит к семейству мареновых, достигает в высоту от 6 до 12 м и имеет очень большие листья, которые располагаются группами по три на конце каждой ветки.

Особенности роста этого дерева можно выразить следующей формулой: N=(Y*12)+4

Она показывает, сколько листьев у дерева. Их точное число обозначается буквой N. Буква У означает возраст дерева в годах. Если решить эту формулу для данного дерева, можно определить точное число его листьев.

Западноафриканское дерево (Schumanniophyton problematicum), знающее правила арифметики.

Почему это так, легко понять, если посмотреть на схематический рисунок этого дерева, сделанный Алле. Это только схема, потому что у реального дерева от каждого узла отходят четыре ветки, а не две, как показано на рисунке. На конце каждой ветки находится три листа, каждый длиной в метр. Таким образом, четыре ветки у каждого узла несут вместе 12 листьев; каждый год, пока дерево не достигнет своего максимального роста (от 5,5 до 6 м), оно выбрасывает по четыре ветки. Цифра 4 в конце формулы прибавляется потому, что верхний побег дерева увенчан четырьмя листьями. На следующий год эти листья превратятся в четыре ветки, а верхний побег увенчают новые четыре листа.

В этой главе рассматриваются два вида Schumanniophyton. На рисунке изображен S. magnificum, у которого очень красивые, большие листья. Листья S. problematicum вдвое меньше, но зато само дерево бывает гораздо выше. Алгебраическая формула верна для обоих видов.